Defined by and named after Leonhard Euler, Euler’s Formula not only changed the way mathematicians analyze functions, polar coordinates, and cartesian coordinates, but it also paved the way for arguably, mathematic’s most beautiful equation: Euler’s Identity.
Euler’s Identity
Termed by Mathematicians as the most beautiful formula in Mathematics, Euler’s Identity takes in irrational values like π and e alongside non-real values like i (Imaginary Number) and outputs -1. When 1 is added to the value, then it returns 0, thus forming a very visually and mathematically appealing function.
This aesthetic equation is an instance of Euler’s Formula, where x (Input Variable) = 1
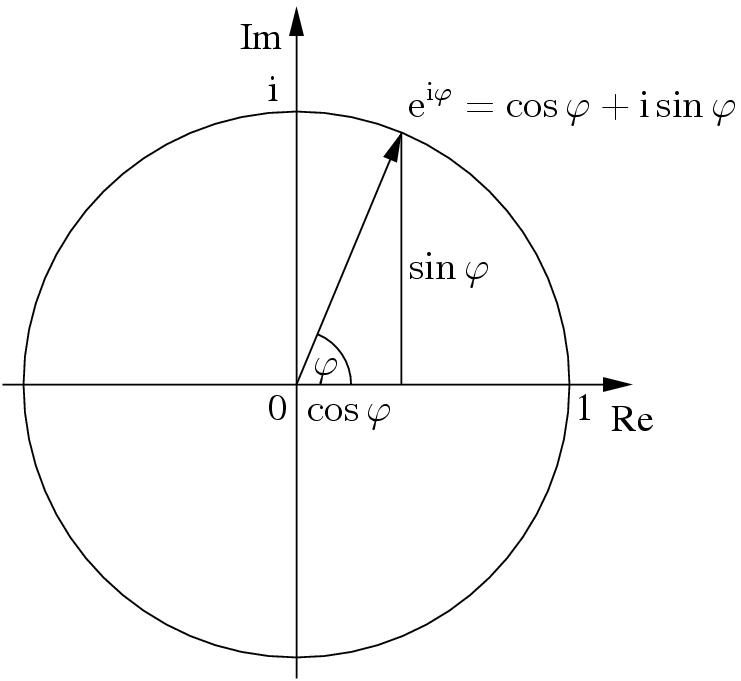
Euler’s Formula: e^(ix) = cos(x) + isin(x)
Euler’s Formula is a very important function when converting from Cartesian to Polar Coordinates and vice-versa. (See the Parametric Equations and Polar Curves Sections for more information) It notably expresses a mathematical relationship between the trigonometric functions cosx and sinx with exponential functions.
But how does this work? -> Derivation of Euler’s Formula
Great question! As noted earlier, Euler’s Identity is just an instance of Euler’s Formula. Euler’s Formula, moreover, can be derived using Maclaurin/Taylor Series expansions! Here is how we can derive Euler’s Formula…


